Setelah kita kemarin mempelajari materi tentang sudut antara
dua garis, sekarang kita akan mempelajari sudut antara garis dan bidang.
Kalian masih ingat hubungan antara garis dan bidang? Yaitu mempunyai kedudukan : garis terletak pada bidang, garis sejajar bidang dan garis bepotongan dengan bidang. Tapi hanya garis yang berpotongan dengan bidang saja yang mempunyai sudut.
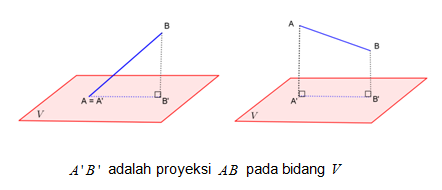
Sebelum kita bahas materi pokok sudut antara garis dan bidang, akan kita ingatkan kembali tentang proyeksi garis pada bidang.
Proyeksi ruas garis ABpada bidang V dapat diperoleh dengan cara menarik masing-masing titik dan sehingga tegak lurus bidang V dan diperoleh A’ dan B’. Ruas garis A’B’ adalah proyeksi ruas garis AB pada bidang V.
SUDUT ANTARA GARIS DAN BIDANG
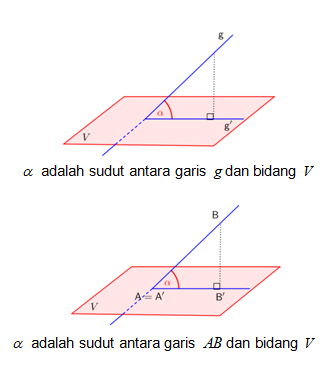
Sudut antara garis g dan bidang V adalah sudut yang dibentuk oleh garis g dan proyeksinya g’ pada bidang V.
Untuk lebih jelasnya dalam menghitung besar sudut antara garis dan bidang mari kita cermati contoh berikut.
Contoh
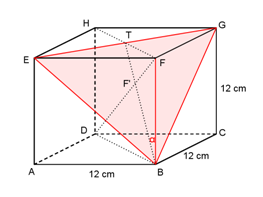
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung :
a). nilai sinus sudut antara rusuk BF dan bidang BEG
b). nilai cosinus sudut antara rusuk AE dan bidang DBG
Jawab :
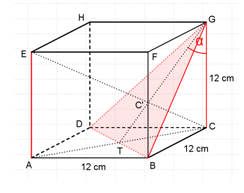
a) Cara menentukan sudut antara rusuk BF dan bidang BEG :
Kita proyeksikan titik B pada bidang BEG yaitu di titik B, kemudian proyeksikan titik F pada bidang BEG dengan cara menarik titik F ke titik D sehingga memotong bidang BEG di titik F’ (yaitu proyeksi F pada bidang BEG).
Jadi proyeksi rusuk BF pada bidang BEG adalah BF’.
Sudut antara rusuk BF dan bidang BEG adalah α = ∠GBF’ atau α = ∠GBT
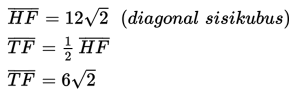
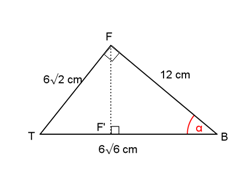Dalam ΔTFB (segitiga siku-siku di F)
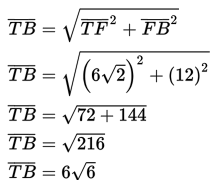Kita ingat rumus luas segitiga :
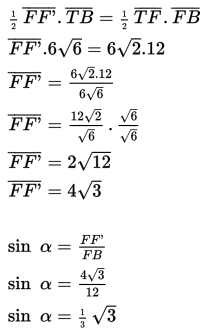b) Cara menentukan sudut antara rusuk AE dan bidang DBG :
Karena rusuk AE dan bidang DBG belum berpotongan, maka AE kita geser ke CG sehingga berpotongan dengan bidang DBG di titik G.
Kemudian kita proyeksikan titik G pada bidang DBG yaitu di titik G sendiri, dan proyeksikan titik C pada bidang DBG dengan cara menarik garis dari titik C ke arah E sehingga garis memotong bidang DBG di titik C’.
Sudut antara rusuk AE dan bidang DBG adalah α = ∠CGC’ atau α = ∠CGT .
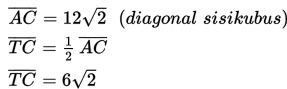
Kalian masih ingat hubungan antara garis dan bidang? Yaitu mempunyai kedudukan : garis terletak pada bidang, garis sejajar bidang dan garis bepotongan dengan bidang. Tapi hanya garis yang berpotongan dengan bidang saja yang mempunyai sudut.
Sebelum kita bahas materi pokok sudut antara garis dan bidang, akan kita ingatkan kembali tentang proyeksi garis pada bidang.
Proyeksi ruas garis ABpada bidang V dapat diperoleh dengan cara menarik masing-masing titik dan sehingga tegak lurus bidang V dan diperoleh A’ dan B’. Ruas garis A’B’ adalah proyeksi ruas garis AB pada bidang V.
Sudut antara garis g dan bidang V adalah sudut yang dibentuk oleh garis g dan proyeksinya g’ pada bidang V.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung :
a). nilai sinus sudut antara rusuk BF dan bidang BEG
b). nilai cosinus sudut antara rusuk AE dan bidang DBG
Jawab :
a) Cara menentukan sudut antara rusuk BF dan bidang BEG :
Kita proyeksikan titik B pada bidang BEG yaitu di titik B, kemudian proyeksikan titik F pada bidang BEG dengan cara menarik titik F ke titik D sehingga memotong bidang BEG di titik F’ (yaitu proyeksi F pada bidang BEG).
Jadi proyeksi rusuk BF pada bidang BEG adalah BF’.
Sudut antara rusuk BF dan bidang BEG adalah α = ∠GBF’ atau α = ∠GBT
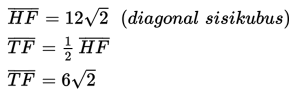
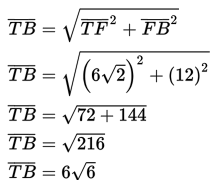
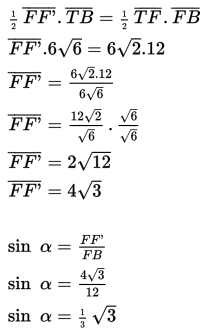
Karena rusuk AE dan bidang DBG belum berpotongan, maka AE kita geser ke CG sehingga berpotongan dengan bidang DBG di titik G.
Kemudian kita proyeksikan titik G pada bidang DBG yaitu di titik G sendiri, dan proyeksikan titik C pada bidang DBG dengan cara menarik garis dari titik C ke arah E sehingga garis memotong bidang DBG di titik C’.
Sudut antara rusuk AE dan bidang DBG adalah α = ∠CGC’ atau α = ∠CGT .
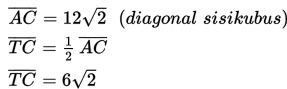
Sign up here with your email
ConversionConversion EmoticonEmoticon