Pada topik sebelumnya, kita pernah mempelajari hubungan
antara garis dengan bidang, yaitu mempunyai kedudukan : berimpit,
sejajar dan menembus. Kalian juga pernah mempelajari topik jarak antara
dua garis sejajar. Dalam topik ini kalian akan mempelajari topik jarak
antara garis dan bidang yang sejajar.
JARAK ANTARA GARIS DAN BIDANG YANG SEJAJAR
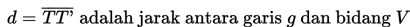
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung jarak antara :
a) rusuk AB dan bidang DCFE
b) ruas garis AL dan bidang DBG
(titik L adalah perpotongan garis diagonal EG dan HF)
Penyelesaian :
 Untuk menghitung jarak rusuk AB ke bidang DCFE, ambil salah satu
titik dari garis AB, misal titik B, kemudian proyeksikan titik B ke
bidang DCFE sehingga diperoleh titik potong B’.
Untuk menghitung jarak rusuk AB ke bidang DCFE, ambil salah satu
titik dari garis AB, misal titik B, kemudian proyeksikan titik B ke
bidang DCFE sehingga diperoleh titik potong B’.
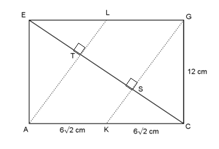
Jarak garis AB ke bidang DCFE adalah BB’ = 6√2 cm.
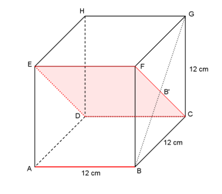
 Untuk menghitung jarak ruas garis AL ke bidang DBG, ambil salah satu
titik pada garis AL, misal titik T, kemudian proyeksikan titik T ke
bidang DBG sehingga diperoleh titik potong S.
Untuk menghitung jarak ruas garis AL ke bidang DBG, ambil salah satu
titik pada garis AL, misal titik T, kemudian proyeksikan titik T ke
bidang DBG sehingga diperoleh titik potong S.
Jarak ruas garis AL ke bidang DBG adalah TS.
 Menurut dalil Intersep yang pernah kita pelajari, bahwa :
Menurut dalil Intersep yang pernah kita pelajari, bahwa :
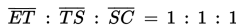 sehingga :
sehingga :
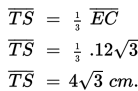
JARAK ANTARA GARIS DAN BIDANG YANG SEJAJAR
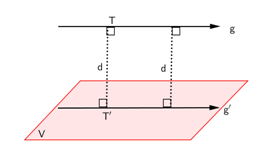
- Jarak antara garis g dan bidang V yang sejajar adalah panjang ruas garis yang diperoleh dari garis g dan proyeksinya (garis g’) pada bidang V.

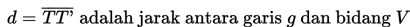
- Langkah-langkah untuk menghitung jarak antara garis g dan bidang V yang sejajar, pada prinsipnya sama dengan mencari jarak antara dua garis sejajar yang pernah kita pelajari sebelumnya, yaitu ambil satu titik pada garis g misal titik T, kemudian proyeksikan titik T pada garis g’ dan diperoleh T’. Jarak antara garis g dan bidang V adalah TT’.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung jarak antara :
a) rusuk AB dan bidang DCFE
b) ruas garis AL dan bidang DBG
(titik L adalah perpotongan garis diagonal EG dan HF)
Penyelesaian :

Jarak garis AB ke bidang DCFE adalah BB’ = 6√2 cm.

Jarak ruas garis AL ke bidang DBG adalah TS.

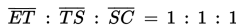
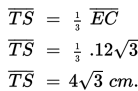
Sign up here with your email
ConversionConversion EmoticonEmoticon